Annales Mathématiques Africaines

On The Synthesis of the Existing Concepts of Good Bifiltrations on an A-Module M and a Criterion for a Bifiltration Φ of M to be F-good in Terms of the Generalized Rees Module of M with Respect to Φ as Module over the Generalized Rees Ring of F, where F is a Crossed Bifiltration on A

Jocelyne AMOUSSOU ¹⁾, Abdoulaye ASSANE ²⁾ et Daouda SANGARE ³⁾

UFR-SFA Laboratoire de Mathématiques et Informatiques
Université Nangui Abrogoua
02 BP 801 Abidjan 02, Côte d’Ivoire

Mathematics Subject Classification: (MSC 2010) 3A02, 13A15, 13A30, 13J30, 16W50, 16W70
Key words: filtration, bifiltration, (I,J)-good bifiltration, (f,g)-good bifiltration, F-good bifiltration, generalized Rees-module of a bifiltration, crossed bifiltration.

Abstract:

For a given commutative unitary ring A and an A-module M, we review in this paper the existing concepts of good bifiltrations on M in the literature. Then we introduce a new and unified concept of F-good bifiltration on M, where F is a bifiltration on a ring A and we undertake some investigations on this new concept. Especially we give a criterion for a bifiltration Φ of M to be F-good in terms of finiteness of the type of the 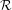(A,F)-module 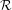(M,Φ), where 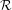(M,Φ) is the generalized Rees module of the A-module M with respect to the bifiltration Φ, F a crossed bifiltration on the ring A and 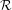(A,F) the generalized Rees ring of F.

Résumé:

Soient A un anneau commutatif unitaire et M un A-module. Dans cet article, nous recensons les concepts de bifiltration bonne sur M existant dans la littérature. Ensuite, nous proposons un concept unifié de bifiltration F-bonne sur M, où F est une bifiltration de l’anneau A, puis nous menons des investigations sur ce nouveau concept. 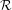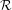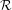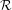En particulier, nous établissons un critère pour qu’une bifiltration Φ de M soit F-bonne en terme de finitude du type du (A,F)-module (M,Φ) où (M,Φ) est le module de Rees généralisé du A-module M relativement à la bifiltration Φ, F une bifiltration croisée de l’anneau A et (A,F) l’ anneau de Rees généralisé de F.