AFRICA MATHEMATICS ANNALS

On Rees Modules of Filtered Modules

Phinées GAHOUROU ⁽¹⁾, Abdoulaye ASSANE ⁽²⁾,
and Daouda SANGARE ⁽³⁾

UFR-SFA Laboratoire de Mathématiques et Informatiques
Université Nangui Abrogoua
02 BP 801 Abidjan 02, Côte d’Ivoire

Mathematics Subject Classification: (MSC 2010): 13A02, 13A30, 13C13
Key words: Filtration, I-good filtration, Rees module.

Résumé:

Pour tout idéal I de l’anneau commutatif unitaire A, les propriétés de l’anneau de Rees de I, R(A,I) = ⊕ _{n ∈ ℕ}IⁿXⁿ et celles d’anneau de Rees généralisé de I, 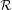(A,I) = ⊕ _{n ∈ ℤ}IⁿXⁿ, ont fait l’objet d’une littérature abondante. Ces deux concepts d’anneau de Rees ont été étendus à un A - module M, essentiellement de deux façons différentes :

(I) R(M,I) = ⊕ _n∈ℕ(IⁿM)Xⁿ et 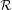(M,I) = ⊕ _n∈ℤ(IⁿM)Xⁿ et

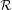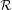(II) R(M,I) = ⊕ _n∈ℕ(IⁿM)⊗ _AAXⁿ et (M,I) = ⊕ _n∈ℤ(IⁿM)⊗ _AAXⁿ Ici nous optons pour les notations du type (II) qui ont l’avantage d’être plus claires par rapport au concept de polynôme à coefficients dans un module. Nous les étendons à une filtration générale φ = (M_n)_n∈ℤ, puis nous menons des investigations sur  les deux modules R(M,φ) = ⊕ _{n ∈ ℕ}M_n ⊗ _A(AXⁿ) et (M,φ) = ⊕ _{n ∈ ℤ}M_n ⊗ _A(AXⁿ) qui sont les modules de Rees de M relativement à φ.

Nous généralisons à une filtration arbitraire φ = (M_n)_n∈ℤ du A - module M, de nombreuses propriétés générales de la filtration I- adique (IⁿM)_n∈ℤ de M, où I est un idéal de l’anneau A. Nous étudions ensuite des conditions de finitude pour certaines filtrations particulières φ de M, en particulier les filtrations de modules qui sont f- bonnes, où f est une filtration donnée de l’anneau A. Cette dernière classe contient les filtrations I- bonnes de modules. Nous suivrons ici les notations  de M. Hermann, S. Ikeda and U. Orbanz [3], Ch.2, paragraphes 8, 9 et 10 et nous généralisons notamment aux filtrations f- bonnes de module (et en particulier filtrations I- bonnes de modules) les résultats de leur section 8.8.

On remarquera que dans la première partie, la filtration φ de M n’est ni I-adique, ni I- bonne, ni f- bonne.