AFRICA MATHEMATICS ANNALS
Article18
Contents > Past issues > Volume 2
Extension aux quasi-graduations sur un semi-anneau des nombres de Samuel de deux idéaux
Youssouf M. Diagana
Soma Ouattara
UFR-SFA, Laboratoire de Math. et Inform.
Université d'Abobo-Adjamé, Abidjan, Côte d'Ivoires
Mathematics Subject Classifications:(MSC2010) 13A15; 13A99.
Key words : Semi-anneaux,
Quasi-graduations, Nombres de Samuel.
Abstract:
Let
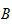 be
a semi-ring and
be
a semi-ring and
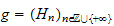 be
a family of sub-monoides of
be
a family of sub-monoides of
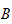 .
.
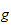 is called a quasi-graduation of
is called a quasi-graduation of
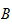 if
if
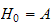 is
a sub-semi-ring of
is
a sub-semi-ring of
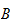 ,
,
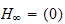 and
and
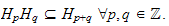
We generalize the numbers of Samuel
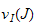 and
and
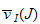 by putting for each semi-ideal
by putting for each semi-ideal
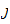 and for
and for
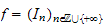 and
and
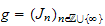 two quasi-graduations of the semi-ring
two quasi-graduations of the semi-ring
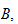
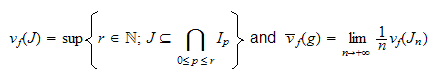
when this limit exists in
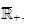
We establish the following results :
1) If
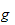 is
decreasing or
is
decreasing or
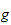 verifies :
verifies :
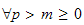
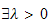 such
that for
such
that for
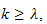
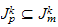
then
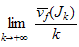 exists
in
exists
in
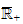 and
one has
and
one has
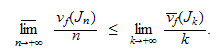
2) Suppose that
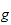 is an AP -quasi-graduation.
is an AP -quasi-graduation.
If
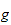 is decreasing or
is decreasing or
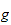 verifies :
verifies :
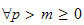
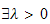 such that for
such that for
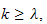
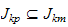 and
and
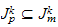 then
then
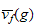 exists in
exists in
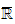 and one has
and one has
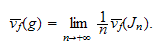
Résumé
Soient
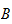 un
semi-anneau et
un
semi-anneau et
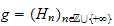 une
famille de sous-monoïdes de
une
famille de sous-monoïdes de
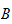 ,
,
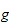 est
une quasi-graduation de
est
une quasi-graduation de
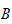 si
si
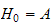 est
un sous-semi-anneau de
est
un sous-semi-anneau de
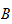 ,
,
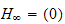 et
et
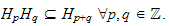
Nous généralisons les nombres de Samuel
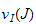
et
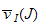 en posant pour tout semi-idéal
en posant pour tout semi-idéal
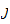 et pour
et pour
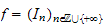 et
et
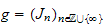 deux quasi-graduations du semi-anneau
deux quasi-graduations du semi-anneau
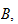
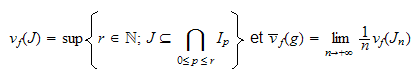
lorsque cette limite existe dans
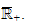
Nous établissons les résultats suivants :
1) Si
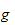 est
décroissante ou si
est
décroissante ou si
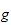 vérifie
:
vérifie
:
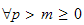
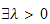 tel
que pour tout
tel
que pour tout
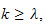
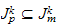
alors
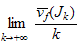 existe
dans
existe
dans
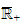 et
l'on a
et
l'on a
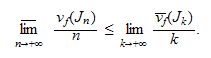
2) On suppose que
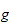 est une AP -quasi-graduation.
est une AP -quasi-graduation.
Si
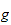 est décroissante ou si
est décroissante ou si
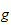 vérifie :
vérifie :
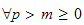
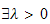 tel que pour tout
tel que pour tout
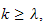
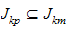 et
et
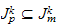 alors
alors
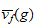 existe dans
existe dans
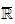 et l'on a
et l'on a