AFRICA MATHEMATICS ANNALS

Analytic Spread of an Axis-quasi-graduation

Eugène D. BECHE ⁽¹⁾, Kouadjo P. BROU ⁽²⁾,
Youssouf M. DIAGANA ⁽³⁾ and N. J. Roland GUIYE ⁽⁴⁾

(1) UFR-ST; Science and Technology Laboratory
BP 20 Man, Côte d’Ivoire, Polytechnic University of Man

(2), (3) and (4)   University of Nangui Abrogoua, UFR-SFA
Mathematics and Computer Science Laboratory
02 BP 801 Abidjan 02, Côte d’Ivoire

Mathematics Subject Classification: (MSC 2010) 13A02, 13A15, 13A30, 13B25, 13F20.
Key words: Analytic Spread, Axis-quasi-graduation.

Abstract:

An axis-quasi-graduation of a commutative ring 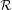is a family g = (G_n)_n∈ℤ∪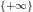 of subgroups of  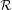such that 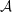= G₀ is a subring of 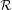, G_∞ = (0) and such that  G_pG_q ⊆ G₀G_p+q, for all p,q ∈ ℤ.

We will show that r elements of 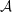G₁ are J-independent of order k with respect to an axis-quasi-graduation g if and only if the two property which follow hold:

- they are J-independent of order k and

- there exists a relation of compatibility between g and the quasi-graduation g_I where I is the 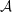-submodule of 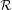constructed by these elements.

Here we give criteria of J-independence in terms of isomorphisms and algebraic independence of elements constructed in quotients of graded algebras. We also give different extensions of the analytic spread of an axis-quasi-graduation of a ring.