AFRICA MATHEMATICS ANNALS

Determination of algebraic points of any degree on 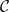₂(7)

Cherif Mamina COLY ⁽¹⁾, Mohamadou Mor Diogou DIALLO ⁽²⁾
and Naima KHELOUFI³⁾

Assane Seck University, Ziguinchor
Ziguinchor 27000, Sénégal

Mathematics Subject Classification: (MSC 2010) -
Key words : Mordell-Weil group, Jacobian, linear system.

Abstract:

We determine geometrically the algebraic points of any degree in ℚ on the curve with affine equation y⁷ = x(x- 1)². This curve has been studied by O. Sall in [1] where the author give a parametrization of cubic points in 2003. we then extend this work to points of degree  4 over ℚ, and in this note we give a generalization, by determining points of any degree on this same curve using a geometric method.