AFRICA MATHEMATICS ANNALS

Largeur analytique d’une bifiltration d’anneau

Bocar Ibrahima TOURE ^(*), Boubacar HAMA ^(**) et Monzon TRAORE ^(***)
Département d’Enseignement et de Recherche en Mathématiques et d’Informatique,
Faculté des Sciences et Techniques (FST), Université des Sciences, des Techniques et
des Technologies de Bamako (USTTB) Bamako, MALI

Mathematics Subject Classification: (2010) 13A02, 13A30, 16W50, 16W70
Key words: filtrations, bifiltrations, bigraduations, fonctions de type polynomial, largeur analytique

Abstract:

In the present paper, we investigate the asymptotic behaviour of the numerical function φ_F : (m,n)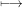dim_k,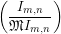
where F = (I_m,n) is an (I,J)- good bifiltration on a nœtherian local ring (A,𝔐,k) and I and J are two ideals of A. Under these conditions the analytic spread of F is defined by λ_𝔐(F) = 2 + degφ_F where degφ_F is the degree of φ_F if φ_F is non null.
In Theorems 1 and 2 of this article, we prove that

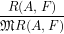λ𝔐(F) = dim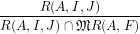 = dim = dim,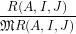

where R(A,F) = ⊕ _{(m,n)∈ℕ²}I_m,nX^mY ⁿ and R(A,I,J) = ⊕ _{(m,n)∈ℕ²}I^mJⁿX^mY ⁿ where X and where Y are two indeterminates.