AFRICA MATHEMATICS ANNALS
Article71
Contents
Independence on Quasi-Bigraduations
of Rings and Analytic Spread
Eugène Deval Béché, Youssouf M. DIAGANA
and Pierre K. BROU
Université Nangui Abrogoua, UFR-SFA
Laboratoire Mathématiques-Informatique
02 BP 801 Abidjan 02 Abidjan, Côte d'Ivoire
Mathematics Subject Classification: (2010) 13A02, 13A15, 13A30, 13B25, 13F20
Key words: Quasi-bigraduations, analytic spread
Abstract:
When f = 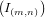
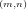 ∈
∈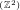 ∪{∞} is a +quasi-bigraduation on a ring
∪{∞} is a +quasi-bigraduation on a ring 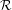 ,
an f+-quasi-bigraduation of an
,
an f+-quasi-bigraduation of an 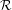 -module
-module 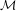 is a family g = (G(m,n)) of subgroups
of
is a family g = (G(m,n)) of subgroups
of 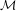 such that G∞ = (0) and I(m,n)G(p,q) ⊆ G(m+p,n+q), for all (m,n) and
(p,q) ∈
such that G∞ = (0) and I(m,n)G(p,q) ⊆ G(m+p,n+q), for all (m,n) and
(p,q) ∈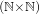 ∪{∞}.
∪{∞}.
We give comparisons of several extensions of analytic spread for compatible +quasi-bigraduations on a ring in term of generalized independences.