AFRICA MATHEMATICS ANNALS

Main menu:

Article70

Contents

Localization Functor S^-1() and Functors ext and tor

Daouda Faye and Mohamed Ben Faraj BEN MAAOUIA
Associated member, Directory of Algebraic Laboratory,
Cryptography, Codes and Applications (LACCA)- UFR SAT
Université Gaston Berger, Saint-Louis (UGB), Sénégal

Mamadou SANGHARÉ
Member, Directory of Algebraic Laboratory,
Cryptography, Algebraic Geometry and Applications
LACGAA - Technologies and Sciences Faculty
Université Cheikh Anta Diop, Dakar (UCAD), Sénégal

Mathematics Subject Classification: (2010)
Key words: Ring, duo-ring, left (right) Ore’s conditions, multiplicatively closed subset, left A-module, ring of fractions, module of fractions, category A-Mod, Mod-A, functors S^-1(), Ext and Tor.

Abstract:

In this paper, unless otherwise stated, B is a duo-ring, A a subring of B, S a multiplicatively closed subset of the ring A satisfying the left (right respectively) Ore’s conditions, S the set of regular elements of S, _AM a left A-module, _BN_A a (B -A)-bimodule (respectively _AN_B a (A-B)-bimodule), S^-1A the ring of fractions of A on S ; particularly, if A is a duo-ring and P is a prime ideal of A then S is the set of regular elements of A - P.
We establish the following results :

1) Isomorphisms of left (S)^-1B-modules :

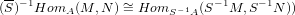
(S-)- 1Hom (M, N) ~= Hom -1 (S-1M, S-1N )) A S A

where M is an (A - B)-bimodule and N a left A-module ;

2) Isomorphisms of left (S)^-1B-modules :

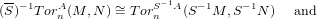
-- -1 (S)-1TorAn(M, N ) ~= TorSn A(S-1M, S-1N ) and

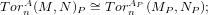
A ~ AP Torn(M, N)P = Torn (MP ,NP );

3) Isomorphisms of right (S)^-1B-modules :

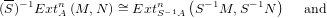
-- ( ) (S)-1ExtnA (M, N) ~= ExtnS-1A S- 1M, S -1N and

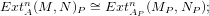
n ~ n ExtA(M, N)P = ExtAP (MP ,NP );

4) If B is noetherian, _BM_A a (B - A)-bimodule, then the functors :

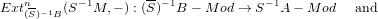
-- Extn-- 1 (S -1M,- ) : (S)-1B - M od → S-1A - M od and (S) B

Tor_n^{S^-1A}(S^-1M,-) : S^-1A - Mod → (S)^-1B - Mod are adjoint.

Back to content | Back to main menu