AFRICA MATHEMATICS ANNALS
Article69
Contents
On a character associated to a representation of Cartan
subgroup of an acceptable Lie group
Gaël NGAMBALI NDZAKIMA
Institute of Mathematics and Physics Sciences
Porto-Novo, Republic of Bénin
Kinvi KANGNI
Department of Mathematics and computer
Université Félix Houphouët Boigny
Abidjan Côte d'Ivoire
Mathematics Subject Classification: (MSC 2010) 22D30, 22E45, 43A40
Key words : Polarization at a representation, π-character, induced representation and
acceptable Lie groups
Abstract:
Let G be a connected semi-simple Lie group, 𝔤 its Lie algebra, j a Cartan
subalgebra of 𝔤, 𝔧c be a complexification of 𝔧 and Jc the analytic Cartan subgroup
associated with 𝔧c. Let Φ denote the set of roots of the pair 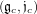 . If α is an element
of Φ, then there exists a holomorphic homomorphism ξα of Jc into ℂ* such
that :
. If α is an element
of Φ, then there exists a holomorphic homomorphism ξα of Jc into ℂ* such
that :
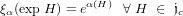
Let π be a representation of 𝔧c in a finite-dimensional vector space V. The homomorphism ξπ associated to the representation π will be called a π-characte.
In this work, some results concernig this character are obtained and proved and after defining a polarization at π, the irreducibility of an induced representation is computed when G is simply connected nilpotent Lie group. The particular case where π is a linear form of 𝔧c has been studied in [6].