AFRICA MATHEMATICS ANNALS

The quasi-spherical transformations

Cornelie MITCHA MALANDA
Université Marien NGOUABI BP : 69, Brazzaville, Congo

Kinvi KANGNI
Université Félix Houphouët Boigny,
22 BP 582 Abidjan 22 Abidjan, Côte d'Ivoire

Mathematics Subject Classification: (MSC 2010) 22E25, 22E27, 22E60
Key words : Quasi-Gelfand pair, quasi-spherical function 

Abstract:

Let G be a locally compact group, K a compact subgroup of G. 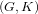is a Gelfand pair if the convolution subalgebra L^1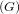♮ of L¹ 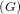that are biinvariant under the action K, is commutative.

Let L_K¹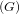 be the algebra of K-invariant L¹-functions on G. L^1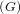♮ is isomorphic to L_K¹(G), then L^1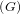♮ is nilpotent is equivalent to the fact that L_K¹(G) is nilpotent.

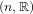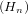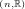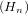Let H_n be the (2n + 1)-dimensional Heisenberg group. The action of the compact subgroup SO of the group of automorphisms Aut of H_n, is not of multiplicity free [1] then L_SO¹ is not commutative and the couple (H_n,SO(n, ℝ) is not a Gelfand pair.

In this work, we will interest in this case where the associated algebra is nilpotent but not commutative and we will construct and study the corresponding spherical transformation which will be called a quasi-spherical transformation.