AFRICA MATHEMATICS ANNALS
Article22
Contents > Past issues > Volume 2
Generalized Samuel Numbers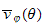 
and
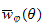
on a Semi-Module
Soma OUATTARA
Université de Cocody, IRMA
08 BP 2035 Abidjan 08, Côte
d'Ivoire
Eric Dago AKEKE
Université de Cocody, UFRMI
22 BP 582 Abidjan 22, Côte
d'Ivoire
Philippe AYEGNON
E.N.S. d'Abidjan 08 BP 10 Abidjan 08, Côte d'Ivoire
Mathematics Subject Classifications: 13A15, 13A18.
Key words : ring, semi-ring, semi-module, filtration.
Abstract:
The Asymptotic Theory of ideals originated with the investigations in a
nœtherian ring
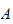of the Samuel number
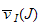associated with each pair
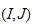of nonnilpotent ideals having the same radical and
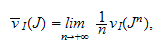
the limit being reached from below and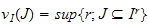 
.
The number
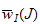is defined in a symmetric situation. In AYEGNON - D.
SANGARE these numbers have been defined for pairs
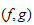where
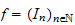and
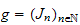are filtrations on a ring
.
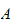In this paper we extend these definitions to generalized Samuel numbers
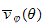and
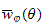where
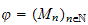and
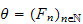are filtrations on the
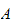-semi-module
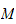by setting :
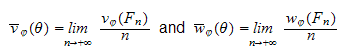
if these limits exist in
.
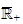It is shown that if
,
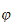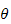and
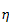are filtrations on the
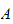-semi-module
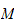such that
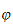is a valuative reduction of
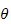then 