AFRICA MATHEMATICS ANNALS

Idéaux irrelevants (resp. relevants), Quasi-filtrations d'un anneau, Caractérisation de la réduction des filtrations par les idéaux irrelevants

S. G. Mete
Ecole Normale Supérieure d'Abidjan

Henri DICHI
Université Blaise Pascal de Clermont-Ferrand II, France

Daouda SANGARE
Université d'Abobo-Adjamé, Abidjan, Côte d'Ivoire

Mathematics Subject Classifications [2010]: 13A02, 13A30 .
Key words : Relevant and irrelevant ideals, filtrations, quasi-filtrations, Reduction of filtrations.

Abstract:

In this paper, we introduce the concept of relevant (resp. irrelevant) ideals for non necessarily homogeneous ideals of 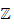-graded commutative rings and also the concept of quasi-filtration of rings which is close to the definition of filtrations of rings. Then we undertake some investigations on these concepts which enable us to give results analogous to some results of D.Rees [5 ]. In the first part we show, in particular, that if 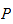is any maximal relevant ideal of a graded nœtherian ring 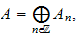then the associated homogeneous ideal 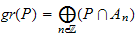is a prime ideal of 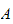. We end this paper by giving a criterion on the reduction of 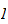- good (resp. strongly nœtherian) filtrations of a local nœtherian ring 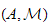in terms of irrelevant ideals of their Rees ring.

Résumé

Dans cette note, nous introduisons le concept d'id\eaux relevants (resp. irrelevants) non n\ecessairement gradu\es d'un anneau commutatif gradu\e de type 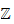et celui de quasi-filtration d'anneau qui est voisin du concept de filtration d'anneau. Nous menons ensuite quelques investigations sur ces concepts qui nous permettent d'\etablir les analogues de certains r\esultats de D. Rees [5 ]. Nous montrons, en particulier, que si 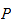est un id\eal relevant maximal d'un anneau gradu\e nœth\erien 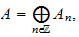alors l'id\eal gradu\e associ\e 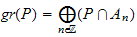est premier. 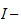Nous terminons cette note par la caract\erisation de la r\eduction des filtrations bonnes (resp. fortement nœth\eriennes) d'un anneau local nœth\erien 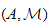par les id\eaux irrelevants de leur anneau de Rees.