AFRICA MATHEMATICS ANNALS

Abstract:

Interior-point methods (IPMs) for semidefinite optimization (SDO) have been studied intensively, due to their polynomial complexity and practical efficiency. Recently, J.Peng et al.peng1,peng2 introduced so-called self-regular kernel (and barrier) functions and designed primal-dual interior-point algoritms based on self-regular proximity for linear optimization (LO) problems.They have also extended the approach for LO to SDO. In this paper we present a primal-dual interior-point algorithm for SDO problems based on a kernel function with quadratic growth rate which was a 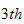in bai2. The kernel function in this paper is self-regular. We derive the complexity analysis for algorithms with large-and small-update methods. 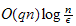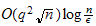The complexity bounds are and , Respectively, which are as good as those in linear case.