AFRICA MATHEMATICS ANNALS
Article17
Contents > Past issues > Volume 2
Largeur analytique d'un couple de filtrations noethériennes
Assane Abdoulaye
UFR-SFA, Labo. Math. et Inform. , Univ. d'Abobo-Adjamé,
Côte d'Ivoire
Mathematics Subject Classifications: (MSC2010) 13A15, 13A30,
13D40.
.
Key words : Filtration, Hilbert-function, quasi-polynomial,
analytic spread.
Abstract:
Let
 be a local noetherian ring,
be a local noetherian ring,
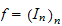 a noetherian filtration of A. Let
a noetherian filtration of A. Let
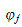 the numerical function defined by :
the numerical function defined by :
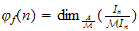
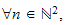
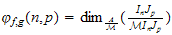 ,
,
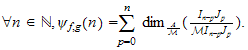
We show that if
 is
is
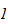 -good
and
-good
and
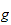
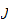 -good,
then
-good,
then
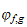 is polynomial type of degree
is polynomial type of degree
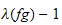 where
where
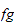 is the filtration
(
is the filtration
(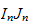 )
and
)
and
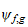 is polynomial type of degree
is polynomial type of degree
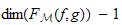 where
where
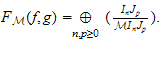
We define then the analytic spread of the couple
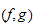 by :
by :
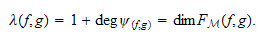
We show with the above hypothesis that :
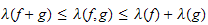 where
where
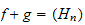 avec
avec
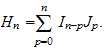
In the same spirit than [1], we show then that if
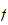 is not
is not
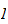 -good
or if
-good
or if
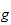 not
not
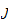 -good,
but if both of them are noetherians, then the function
-good,
but if both of them are noetherians, then the function
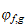 (resp.
(resp.
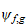 ) is quasi-polynomial and all the polynomials components of the
qasi-polynomial associated have the same degree wich is
) is quasi-polynomial and all the polynomials components of the
qasi-polynomial associated have the same degree wich is
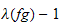 (resp
(resp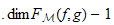 if
if
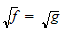 ).
).
Résumé
Soient
(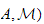 un anneau local noethérien
un anneau local noethérien
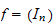 une filtration noethériennne de
une filtration noethériennne de
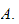
Soit
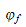 la
fonction numérique définie par
la
fonction numérique définie par
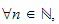
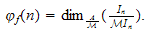
La fonction
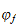 si elle n'est pas nécessairement de type polynomial, est néamoins
quasi-polynomial d'après H.Dichi et D.
Sangaré
si elle n'est pas nécessairement de type polynomial, est néamoins
quasi-polynomial d'après H.Dichi et D.
Sangaré![$\left[ 6\right] $](files/abstract17__40.png) .
.
La largeur analytique de
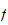 est définie par :
est définie par :
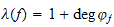 .
.
Mais contrairement aux fonctions de type polynomial, on a pas en général d'information ni sur le degré, ni sur les coefficients dominants des polynômes composantes du quasi-polynôme associé à une fonction quasi-polynomiale générale.
Dans cet article, pour tout couple
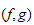 de filtrations noethériennnes sur l'anneau local noethérien
(
de filtrations noethériennnes sur l'anneau local noethérien
(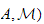 ,
avec
,
avec
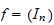 et
et
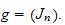 On considère les fontions numériques
On considère les fontions numériques
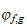 et
et
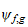 définies comme suit :
définies comme suit :
pour tout
(n,p)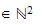 (resp.
(resp.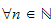 )
)
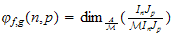 ,
,
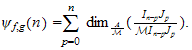
On montre que si
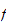 est
est
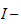 bonne
et g est
bonne
et g est
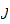 -bonne,
alors
-bonne,
alors
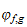 est de type polynomiale de degré
est de type polynomiale de degré
 où
où
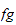 est la filtration
(
est la filtration
(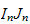 )
et
)
et
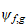 est de type polynomial de degré
est de type polynomial de degré
 où
où
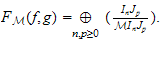
On définit alors la largeur analytique du couple
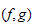 de filtrations où
de filtrations où
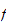 est
est
 bonne
et g est
bonne
et g est
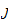 -bonne
comme étant le nombre :
-bonne
comme étant le nombre :
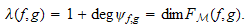
On montre en particulier que sous les hypothèses
précédentes
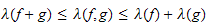
où
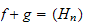 avec
avec
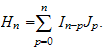
Dans le même esprit que [1], on montre ensuite que si
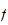 n'est pas
n'est pas
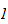 -bonne
ou si
-bonne
ou si
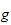 n'est pas
n'est pas
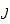 -bonne,
mais si elles sont noethériennes toutes les deux, alors la fonction
-bonne,
mais si elles sont noethériennes toutes les deux, alors la fonction
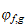 (resp.
(resp.
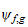 )
est quasi-polynomiale et tous les polynômes composantes du
qasi-polynôme associé ont le même degré qui est
)
est quasi-polynomiale et tous les polynômes composantes du
qasi-polynôme associé ont le même degré qui est
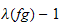 (resp
(resp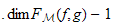 si
si
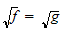 ).
).