AFRICA MATHEMATICS ANNALS

Main menu:

Article14

Contents > Past issues > Volume 2

On Differential Operators 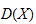's automorphisms group in $Aut_{k}(A_{1}(k))$

Kouakou M. K.
UFR Mathématiques et Informatique
Université de Cocody, 22 BP 582 Abidjan 22, Côte d'Ivoire

Tchoudjem A.
Université Claude Bernard Lyon I, Institut Camille-Jordan, France

Abstract:

Let 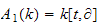be the first algebra over a field 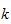of characteristic zero and 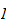a right ideal of 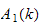$A_{1}(k)$ . The subgroup of Stafford associated to 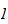denoted 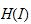is :
MATH
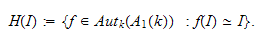
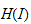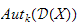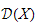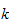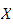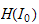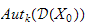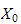By J.T. Stafford in [5], it is known that subgroups are isomorphic to automorphisms groups , where $\QTR{cal}{D}(X)$ is the -algebra of differentials operators over an algebraic affine curve . Due to Stafford, it is known at this step that the $H(I_{0})$ isomorphic to where $X_{0}$ is the well-known algebraic affine curve defined by the equation: 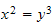$x^{2} = y^{3}$ , is equal to its own normalizer in .
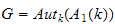We will show in this paper that for any ideal 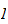, 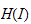is equal to its own normalizer, precisely we show that for any right ideal 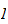and 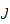non principal, one has :
MATH
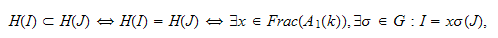
from which it follows that 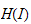is equal to its own normalizer in .
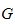